How To : Animate Cranks and Pistons in Maya

figure 1

A recent project I worked on required the modelling of an animating crank and a piston similar to those used by steam locomotives. Engines that use pistons as a power source need a way of converting the back and forth (reciprocating) linear piston motion into rotational motion. Cranks are used to do this and these are connected to points that are offset from the main rotational axis on what is called the crankshaft, and these in turn are connected to the pistons. The crankshaft is the part that receives the rotational energy. The system will also work in reverse, turning the rotational movement into linear.

So that's how it works in the real world, so how do we translate this into Maya?



For our purposes, we'll use the rotating crankshaft to drive the animation and there's a few ways we can go about this; using constraints, using set driven keys or using expressions. Using constraints will only get you part of the way and as you develop it, you'll find there'll be an issue with cyclic dependencies. So you'll constrain the piston to the rod, but you also need to constrain the rod to the piston and even using controllers or parenting this will still cause the same cyclic dependencies that result in evaluation errors and nasty jittering. I've tried all sorts of ways but couldn't create a viable solution. So another way would be to use set driven keys, but you'll need to use a lot of them in order to describe the motion accurately. At best you'll only achieve an approximation. However, if cheap and nasty works in the context of your requirements then fine, use whatever works. If you want to know how to do it properly, read on.

Expressions (unfortunately) are the only way we can solve this accurately. It's not cheap (you'll need to invest in some maths) but the result is a perfect system that's smooth and completely predictable.

I don't usually advocate the use of expressions and try and avoid them like the plague; they can be too rigid and restrictive in an animated workflow, locking nodes onto coded 'rails' and initiating behaviours that are hard to break away from. However, a system such as a crank and piston is ideal for this method; the system is completely closed (unless you plan to decompose the system later) and is a perfect example of how we can use expressions correctly and mathematically model the reciprocating motion. Just because I don't like using them, doesn't mean I won't and after this exercise I must say I am feeling just a little bit of love for Maya's expressions.

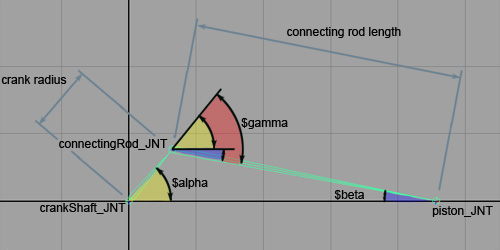
The crankshaft is the assembly that rotates, the piston is the assembly that only moves in one axis, and the connecting rod is the linkage that connects them both together and transfers the rotational energy into linear motion.

In order to work out the position of the piston, we'll need to find out how much the connecting rod needs to be rotated by in order to keep the piston horizontal. Once we have that angle, we've got our solution, and this solution comes from our mathematical knowledge of triangles.

So here's the investment part, the maths...

figure 2

As the crankShaft_JNT rotates ($alpha), we need to work out the relative angle ($gamma) needed for the connectingRod_JNT to let the piston_JNT remain in a fixed horizontal axis. In our case, the piston_JNT can only move in the X axis. We know the crank radius and the connecting rod length, so we can use triangles and trigonometry to find $gamma by application of the Sine Rule to find $beta.

crank radius / sin $beta = connection rod length / sin $alpha

Re-arranging this equation to find $beta..

$beta = arcsin (connection rod length / (sin $alpha * crank radius))

And using another rule; pairs of angles with parallel lines (transversals), we can find $gamma(red on figure 2) from $alpha (yellow on figure 2) and $beta (blue on figure 2).

$gamma = $alpha + $beta

Note, we'll have to negate $gamma as an anticlockwise angle is needed. See the right hand grip rule for how to work out which way something will rotate.

Below we have an example script to create this system using Maya's joints and an expression which will explain it further. Cut and paste it into Maya's script window and execute it.

import maya.cmds as mc

#settings
crankRadius = 1
connectionRodLength = 4
expressionName = 'crank'

# Create the components
mc.joint(n='crankShaft_JNT', p=(0, 0, 0))
mc.joint(n='connectingRod_JNT', p=(crankRadius, 0, 0)  )
mc.joint('crankShaft_JNT', e=True, zso=True, oj='xyz')
mc.joint(n='piston_JNT', p=((connectionRodLength + crankRadius), 0, 0) )
mc.joint('crankShaft_JNT', e=True, zso=True, oj='xyz' )

#create throttle attribute on the crank
mc.addAttr('crankShaft_JNT', longName = "throttle", attributeType='double')
mc.setAttr('crankShaft_JNT.throttle', edit=True, keyable=True)
mc.setAttr('crankShaft_JNT.throttle', 200)

#expression syntax
exp = 'crankShaft_JNT.rotateY = time * crankShaft_JNT.throttle;'
exp += 'float $alpha = crankShaft_JNT.rotateY;'
exp += 'float $beta = asind((%s * sind($alpha) / %s));' % (str(crankRadius), str(connectionRodLength))
exp += '$gamma = -1 * ($beta + $alpha);'
exp += 'connectingRod_JNT.rotateY = $gamma;'

#create the expression
mc.expression(string = exp,name = expressionName);

You should see the the following result in the top view after hitting play..

figure 3

I've connected the crankShaft_JNT.rotateY to the time attribute, and together with this I've used a throttle attribute on this joint to control the speed. The expression should be simple to follow using the simple maths above as reference.

So there you have it, a completely perfect simulation of a crank and piston. Just parent constrain your geometry, group it all and move into position.

Please feel free to drop me a line if you need anyhing else from this.